Четвертое измерение потребовалось для описания релятивистских эффектов, для этого в «континуум» была добавлена четвертая ось.
Правда, добавление этой оси наглядно возможно лишь в случае, если наше физическое пространство представлено либо прямой («одномерное пространство»), либо плоскостью, то есть «двумерное пространство», а временная ось перпендикулярна (нормальна, ортогональна) к этой плоскости. Тогда можно наглядно демонстрировать такие модели, как «световые конусы», и прочие эффекты Лоренца, Пуанкаре, Минковского, Эйнштейна, и других ученых, которые работали над этими теориями.
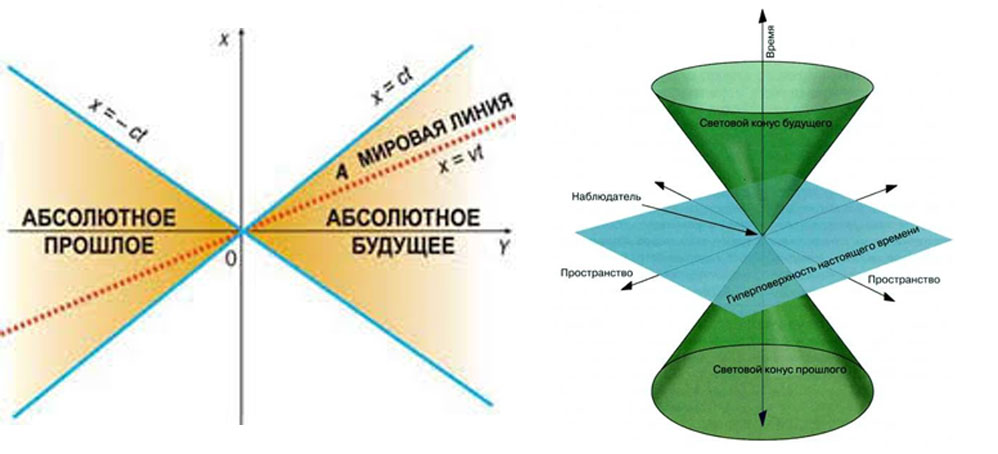
В случае нашего, то есть трехмерного пространства, ось времени добавлять уже некуда, и тогда следует объяснение, что мы просто не можем представить себе 4-х мерное пространство, а также прочие «n-мерные пространства»
На данный момент можно уверенно утверждать, что «4-ти мерный континуум», иначе говоря «Пространство-время» имеют под собой реальное основание, и многократное подтверждение успешными экспериментами по проверке Теории Относительности Энштейна.
С другой стороны, такие понятия, как «мерности», в целом являются продуктом интеллектуальной деятельности человека, как разумного существа, описывающего мир с помощью им же выдуманных инструментов. К примеру, наук Математика и Геометрия. Наблюдаемое нами пространство как сущнось вообще не имеет никаких «осей», а координаты в пространстве можно задавать не только в Декартовой системе координат, а цилинидрическими, сферическими и прочими координатами.
Но для описания поведения реальных тел декартовой системы мало — помимо координат, в каждой точке для описания события необходимо добавлять другие параметры, например можно в каждой точке указывать температуру среды, и тогда это будет «поле температур», или указывать величину напряженности силового поля. Но в любом случае, все события протекают во времени. Так куда нам направить ось времени, если все пространственные оси заняты?
Для начала, в каждой интересующей нас точке можно «разместить» часы, которые будут показывать ход времени в конкретной точке.

Только не надо забывать, что часы эти будут показывать состояние часов, во всех этих точках, относительно какой-то выбранной системы отсчета, да и то если была возможность предварительно синхонизировать часы во всех этит точках. Это возможно сделать локально, к примеру в пределах Солнечной системы, но на космических масштабах такая синхронизация невозможна, и лишена смысла. Но данная статья не о синхронизации часов.
Согласно ТО и ОТО, природа гравитации обусловлена искривлением 4-х мерного континуума под дествием массы, на сами же предметы не воздействует никакая сила. Они продолжают движение вдоль оси времени в частности, и по «континууму» в общем по кратчайшему пути — по «геодезическим линииям» в 4-х мерном пространстве. Однако по этому поводу имеются некоторые сомнения:
«Выбор пространства для ОТО породил парадокс, пугающая сила которого заставляет всех закрывать на него глаза. В геометрическом 4-х мерном пространстве всякое движение отсутствует, т.к. все 4-е координатные оси являются протяженностью. В этом пространстве возможны только геометрические фигуры и тензорные муляжи. В нем нет места наблюдателю. Похоже, этого Эйнштейн так и не понял, как не понимают все его последователи. О каком инерционном движении в искривленном пространстве писал Эйнштейн, и продолжают писать его последователи, остается загадкой. В пространстве Эйнштейна любое реальное движение по инерции или под действием сил гравитации, отображается неподвижной и жесткой мировой гиперлинией.
У Минковского, который придумал специализированное пространство, для удобства исследования свойств объективного мира с помощью света, как информационного посредника всех наблюдаемых взаимодействий, мировые линии строились и исследовались с помощью пространства Евклида. Человек по-другому просто не может. Чтобы исследовать движение реальной материальной точки с помощью 4-х мерного пространства, нужно извлечь интересующую часть пространственного муляжа (или интересующей проекции) из этого пространства и ухитриться поместить её в пространство Евклида, т.е. в реальное пространство.
Изобретение Минковского является инструментальным пространством, оно сродни логарифмической линейке: установил рейку, подвинул ползунок – и получи результат. В инструментальном пространстве Минковского всё очень похоже: направил, отложил, совместил. Попала точка внутрь конуса – значит, событие могло случиться; а не попала точка в конус – значит, такого события не могло быть в принципе. События не было – а точка есть. Пространство Минковского – это не преобразованное реальное пространство, пусть и очень экзотическое; это совсем иное, это придуманное мертвое вспомогательное пространство — инструмент.
Непонимание этого момента является ошибкой многих исследователей, пытающихся оперировать в многомерном пространстве. Авторы многомерных пространств, описывая их свойства, постоянно путаются, приписывая гиперпространству свойства реального пространства. Ошибка проявляется в виде нелепого конечного результата, являющегося следствием одновременного применения двух несовместимых стандартов к одному объекту. В результате всегда получается абракадабра.
Ярким примером такой абракадабры может служить интерпретация пространства Эйнштейна. Два идентичных объекта, вылетевших из одной точки с разными скоростями, будут двигаться по разным траекториям, определяемым кривизной пространства. Одна и та же кривизна пространства по-разному искривляет траекторию спутника Земли и фотона, пролетающего мимо спутника. Получается, что кривизна пространства, которая в ОТО определяет движение по инерции, зависит от скорости объекта, которой в пространстве Эйнштейна нет. А как ввести скорость в тензор импульса, учитывая её относительность, рекомендации отсутствуют.
Движение реальной точки (релятивистского протона) описывается в пространстве Эйнштейна мировой линией. Даже зная положение протона на мировой линии в заданный момент, нельзя определить, где он будет в следующий момент. Методики, разработанные для линейных пространств, требуют построения перпендикулярных и параллельных прямых. Но в кривом пространстве Эйнштейна нет прямых линий, нет, и не может быть, прямолинейных ортогональных координат. У пространства Эйнштейна нет удобного математического инструментария в релятивистской области, для которой ОТО и разработана. Уравнения Эйнштейна приблизительно справедливы лишь в малой области, окружающей точку. Попытка применить уравнения ОТО к релятивистским объектам вскрывает следующее обстоятельство, оказывается кривизна пространства зависит от относительной скорости каждой пары объектов, и каждое тело формирует множество мировых линий в множестве индивидуальных, 4-х мерных пространствах. В этой ситуации практика ИСО с ортогональными координатами, становится абсолютно беспомощной. На ум приходит стохастическая геометрия, но зачем человечеству искусственные трудности.
Если обобщить все сказанное выше, то ОТО все сводит к статической геометрии форм, не объясняя, почему и зачем все сущее непрерывно движется вдоль «оси времени», и что за «вечный двигатель» отвечает за это движение. Однако, игнорировать факт подтверждения предсказанных теорией относительности эффектов замедления времени вблизи массивных тел, или собственного времени тел, находящихся в движении, мы также не можем.
Возможно, «четырехмерный континуум» является не описанием реального пространства, а красивой моделью, интерпритацией, в которой меру скорости проистечения физических процессов заменили на «ось времени».
